Porosity of Petroleum Reservoir Rocks
Porosity of Petroleum Reservoir Rocks
Sedimentary rock consists of grains of solid matter with varying shapes that are more or less cemented and between which there is empty space (Figure 2.1). It is these empty spaces that are able to contain fluids such as water or liquid or gaseous hydrocarbons and allow them to circulate.
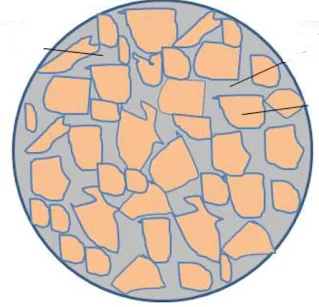 |
Figure 2.1 Porosity |
where ф is porosity, Vp is
pore volume [cm3] and Vb -is total (bulk) volume [cm3].
Alternatively, we can subtract the
matrix volume (in this case, the ice cubes) from the total volume and divide it
by the total volume to obtain the porosity, as shown in the following equation:
where Vg is the matrix volume (grain volume) [cm3].
Overall, we can say that:
Reservoir rocks are porous and
contain fluids in their pores, as shown in Figure 2.2. Porosity
measurement from a core is part of routine core analysis RCAL. When we use the
term "core," we usually refer to a cylindrical rock sample with a
width and length of a few centimetres.
In addition, when dealing with rocks, we often refer to the matrix volume as the grain volume (Vg) and the total volume as the bulk volume (Vb). Note that the fractional porosity value is often multiplied by 100 to make it a percentage; however, it should always be a fraction when used in calculations. The porosity of reservoir rocks usually ranges from 5% to 40%. Table 2.1 shows typical porosity values for different reservoir rocks. The porosity of rocks within a reservoir indicates how much oil and/or gas is stored in that reservoir. Therefore, finding the porosity of the reservoir beforehand is important for engineers because it helps them estimate how economically viable that reservoir is and how many resources should be invested in it.
|
Table 2.1: Typical porosity values in reservoir rocks. |
|
|
Rock Type |
Range |
|
Loosely consolidated sands |
35–40% |
|
Sandstones |
20–35% |
|
Well-cemented sandstones |
15–20% |
|
Limestones |
5–20% |
Classification of Porosity
Porosity has two types of classifications: geological and
engineering.
Geological Classification of Porosity
In terms of geological classification, porosity is classified into
two subdivisions: primary and secondary. Primary porosity is the
original porosity that develops during the deposition of the material. Primary
porosity can be either intergranular or intragranular (Figure 2.3).
Intergranular porosity is the porosity between grains, while intragranular
porosity is the porosity within the grain itself. Intergranular porosity forms
the majority of the porosity of the rock. Secondary (induced) porosity
is developed after deposition by geological processes which result in vugs and
fractures.
 |
Figure 2.3: Schematic showing the
difference between intergranular and intragranular porosities. |
Engineering Classification of Porosity
In terms of engineering
classification, porosity can be subdivided into two categories: total
and effective. Total porosity (фt) is the total pore volume
of the rock divided by the bulk volume. On the other hand, effective porosity
(фe) is the interconnected pore volume divided by the bulk volume.
Ineffective porosity is the isolated pore volume divided by the bulk volume. Figure
2.4 shows the difference between effective and ineffective porosity.
Usually in sandstones, фt = фe as they are relatively
homogeneous rocks. Carbonate and dolomite rocks, on the other hand, usually
have фt > фe since carbonates are typically
heterogeneous. As petroleum engineers we are mainly interested in the effective
porosity since hydrocarbons can only flow through connected pores.
 |
Figure 2.4: Schematic showing the
difference between porosity subdivisions: total, effective, and ineffective. |
Calculation of Porosity
If we consider a cubic packing of
spheres (ideal situation) and look at a cube section as shown in Figure
2.5, the length of the cube is 2r, where r is the radius of the sphere.
Thus, the bulk volume of the cube will be:
Vb = (2r)3 = 8r3
The matrix volume in this case is
represented by the volume of the spherical portions in this cubic segment. We
have eight equal portions of one-eighth of a sphere in this cube, thus:
The porosity then becomes:
∅=(Vb-Vg)/Vb =1-π/6=0.476
We can conclude that the grain size
does not affect the porosity of the rock (as all the radii in the equation
cancel out). In other words, having large spheres or small spheres will lead to
the same porosity as long as they are all of the same size and have the same
packing (Figure 2.6). A value of 0.476 is the highest achievable
porosity, and naturally you will always come across a porosity value less than
this.
 |
Figure 2.5: Schematic showing (a) a
cubic packing of spheres from which (b) a subset cube is selected and then (c)
analyzed. |
 |
Figure 2.6: Schematic showing (a)
the large particle size and (b) the small particle size. Both have the same
porosity as the particle size does not affect the porosity value. |
Factors Affecting Porosity
Porosity can be affected by either primary or secondary factors.
Primary Factors
Particle Packing
Different packing arrangements lead to different porosities, as shown in Figure 2.7. A cubic packing of matrix (Figure 2.7a) leads to a highest possible porosity of 47.6%, as discussed previously, while rhombohedral packing of spheres (Figure 2.7b) leads to a highest possible porosity of 26.0%, which is lower than the previous case.
 |
Figure 2.7: Different packing leads
to different porosities; (a) cubic packing has 47.6% porosity and (b)
rhombohedral packing has 26.0% porosity. |
Sorting
Particles are referred to as “well
sorted” when they are all of the same size while they are poorly sorted when they
are of different sizes (Figure 2.8). Well-sorted particles result
in a higher porosity compared to poorly sorted particles.
Secondary Factors
Cementing materials
The presence of more cementing
materials means less porosity as there is less void space available for the
storage of hydrocarbons.
Overburden pressure (compaction)
Overburden pressure will lower the
pore volume of the rock, leading to lower porosity.
Vugs, dissolution, and fractures
These are formed after deposition
and will increase the porosity of rocks. Dissolution is when the minerals
dissolve over time. Some minerals will dissolve in water. Vugs are large pores
formed by dissolution. Fracture is a break or separation in a rock formation.
Laboratory Measurements
There are usually two methods of
measuring porosity. We either measure it using laboratory measurements (RCAL)
at the centimeter scale or using wireline logging at the meter scale.
There are several methods of finding
porosity in the laboratory. However, we will focus on the two most common
techniques, which are the fluid displacement and gas expansion using a gas
porosimeter. All the rocks used in the laboratory core analysis are rocks
extracted from a reservoir using coring performed by a downhole instrument, as
shown in Figure 2.9.
 |
Figure 2.9: Schematic showing a
downhole instrument used to collect rock samples from the reservoir (sidewall
coring tool). |
Fluid Displacement
The concept of fluid displacement is
based on mass/material balance. In this technique, we weigh a dry core and
measure the dimensions, specifically the diameter and length of the core. Then,
we vacuum saturate the core with water or brine (salt water), for instance, to
make sure that the water has filled all the pore spaces and no air is trapped
in the core (Figure 2.10). The core is then weighed to find the
saturated weight. Subtracting the saturated weight from the dry weight, we
obtain the weight of the water in the pore spaces (Figure 2.11).
By dividing the weight of the water by the density of the water, we obtain the
pore volume:
where Ws is the weight of
the core saturated with fluid [g], Wd is the dry weight of the core
[g], and ρ is the density of the fluid [g/cm3]; since the fluid in
this case is water, the density is 1 g/cm3.
From the displacement method, we can
also find the bulk volume of irregular shapes. Let us consider a rock with an
irregular shape as shown in Figure 2.12. In order to measure the
volume, we need to coat the surface of the rock with an insulating material
such as paraffin (ρ = 0.9 g/cm3) to prevent the fluid we are using
to enter the pores. However, before that we need to measure the dry weight of
the rock sample and the weight of the core with the paraffin. The difference
between the two weights divided by the density of paraffin is the volume of the
added paraffin. This volume will then be subtracted from the final volume
calculation. After performing all these steps, we can find the volume of the
rock using two methods:
1.
We
can record the initial volume of water in the graduated cylinder, and then
record the new volume of water after submerging the rock. The difference
between the new volume and the initial volume is the volume of the rock.
However, we also need to subtract the volume of the paraffin to obtain the
actual bulk volume of the rock (Figure 2.12a).
2.
We
can also use the Archimedes’ principle to find the bulk volume of the rock (Figure
2.12b):
Wdf =
Wr − Wa
where Wdf is the weight
of the displaced fluid [g], Wr is the dry weight of the core or the
weight of the core at the initial conditions before submerging (real weight)
[g], and Wa is the weight of the core after submerging it in the
fluid (apparent weight) [g]. Wa is less than the real weight due to
buoyancy forces. Note that we need to suspend the core in order for buoyancy
forces to act on the core. Finally, in order to measure the bulk volume, we
need to use the following equation:
where ρ is the density of the fluid
in which the core is submerged [g/cm3], which in this case is water,
and Vcoat is the volume of coat used, usually paraffin [cm3].
Note that Vcoat can be measured by subtracting the weight of the
sample with the coat from the weight of the sample without the coat and divide
the product by the density of coat used, i.e., paraffin.
The Gas Expansion Method
The second method used to measure
porosity is the method of gas expansion using a helium porosimeter, which
relies on Boyle’s law:
P1V1
= P2V2 )
In this method, we usually use
helium as it has a low molecular weight and so can easily enter the smallest
pore spaces, which will lead to the most accurate results. We use the system
shown in Figure 2.13a which consists of two chambers separated by
a valve, with a pressure sensor in the first chamber. Chambers 1 and 2 should
be of fixed volumes. To break down the process, we need to understand the
following:
We fill chamber 1 with helium and
then record the pressure; thus, we have P1 and V1 as shown in Figure 2.13b.
If we open the valve to chamber 2,
as shown in Figure 2.13c, then Boyle’s law becomes:
P1V1
= P2(V1 + V2) )
If we consider an actual case where
we have a rock inside chamber 2 (Figure 2.13d), then Boyle’s law
becomes:
P1V1
= P2(V1 + V2−Vm) )
In this case, helium will access all
the chambers and the pore spaces. The only space helium will not access is the
matrix volume as it is not porous; using this technique, we can calculate the
porosity.
We will calculate Vm from
the equation above, as V1 and V2 are constants and P1
and P2 will be read from the equipment. After finding Vm
and also knowing the bulk volume of the core, which is easy to measure, we can
calculate the pore volume as Vp= Vb – Vm and
the porosity is equal to Vp divided by Vb.
It is important to mention that both
the fluid displacement and gas expansion tests measure the effective porosity
as fluids can only access the connected pores.
Measurement of grain volume is
easily completed using a type of Boyle's law apparatus illustrated in Figure.2-13,
where a clean, dry sample is placed in a chamber of known volume. This chamber
is isolated from the upstream pressure chamber, which is also of known volume.
The upstream pressure chamber is charged to a pressure of approximately 100-psi
and then isolated. The connection between the pressure chamber and sample chamber
is opened, and gas expands into the sample chamber, causing a drop in the
original reference pressure.
If the volumes of the pressure and
sample chamber are known, the grain volume may be calculated using the measured
pressure.
Where V1
-reference cell volume, V2 -sample cell volume, Vg -grain
volume of sample, P1 -initial pressure in reference cell, and P2 -final pressure
in system
Further, the cell volumes Vc
and VR are difficult to measure with the desired accuracy. This
instrument is, however, easily calibrated with precisely known solid volumes
such as steel balls. If all measurements are then started at the same P1,
it is a simple matter to obtain Vs from a previously determined
calibration plot of Vs vs P2.
Grain volume may also be calculated
from
Equation (-) is often used with the
typical value for
Grain/Matrix Density
Grain/matrix density [g/cm3]
is also considered a part of the RCAL. In order to measure it, we need to know
the bulk volume, the weight of the rock sample, and the pore volume. Finding
the matrix density can easily be a part of porosity measurement as only the
weight of the sample will be required. After we measure the porosity, we can
find the matrix volume and hence the matrix density can be obtained through the
following equation:
where ρg is the density
of the matrix [g/cm3], Wd is the weight of the matrix or
the dry weight of the core [g] as the density of air is assumed to be
negligible; Wg = Wd (dry weight of the entire core), and
Vg is the volume of the matrix [cm3], which is the bulk
volume minus the pore volume (Vb – Vp).
Typical matrix densities of
different rock types are shown in Table 2.3.
|
Table 2.3:
Typical matrix densities for different rock types. |
|
|
Lithology |
ρm [g/cm3] |
|
Sandstone |
2.65 |
|
Limestone |
2.71 |
|
Dolomite |
2.87 |
The Russell method utilizes an
especially designed volumeter (Figure. 2-10), and the bulk volume
and grain volume are determined volumetrically. The porosity determined is total
porosity.
 |
Figure. 2-10 Russell volumeter for
determining grain and bulk volumes of
|
rock samples. |
Consider a bulk volume of rock with
a surface area of one acre and a thickness of one foot. An acre-foot is the
basic rock volume measurement used in oil field calculations. It is also
standard practice to express all liquid volumes in terms of barrels. The
following conversion factors are useful:
acre
= 43,560 ft2= 4,047 m2
1
acre-ft= 43,560 ft3 = 4,047 m2
1
bbl = 42 gallon=5.61 ft3 = 0.159
1
acre-ft = 43560/5.61 = 7758 bbl
Consider a reservoir with an area of
A acres and an average thickness of h feet. The total bulk volume of the
reservoir can be determined from the following expressions:
or
where A is surface area of
reservoir, [acres], and H is average thickness of formation, [feet]
then it is obvious that the pore
space within a rock is equal to
The reservoir pore volume in cubic
feet
The reservoir pore volume in barrels:
as showing by Figure.2-13
the volumetric equation of oil in place
Where N- Stock-tank oil in place, [bbl/acre-ft],
So - fraction of pore space occupied by oil (the oil saturation), Sw
- the water saturation, and Bo - the formation volume factor for the
oil at the reservoir pressure, reservoir barrel/stock tank barrel, or bbl/STB.
It is necessary to determine Sw
some water will always exist within the reservoir rock and that its volume must
be subtracted from the space available for oil. This water is commonly called
connate water and is assumed to be incompressible in this equation.
It is assumed that the pore space
will be occupied by either oil or water, and that no free gas will be present.
Consequently, the equation as given must be applied to the reservoir at or
above the bubble point and is generally used to compute the initial oil in
place.
Averaging Porosity
The reservoir rock may generally
show large variations in porosity vertically but does not show very great
variations in porosity parallel to the bedding planes. In this case, the
arithmetic average porosity or the thickness-weighted average porosity is used
to describe the average reservoir porosity. A change in sedimentation or
depositional conditions, however, can cause the porosity in one portion of the
reservoir to be greatly different from that in another area. In such cases, the
area-weighted average or the volume-weighted average porosity is used to characterize
the average rock porosity. These averaging techniques are expressed
mathematically in the following forms:
Arithmetic average ∅=(∑▒∅i )/n
Thickness-weighted average ∅=(∑▒〖∅i×hi 〗)/hi
Areal-weighted average ∅=(∑▒〖∅i×Ai 〗)/Ai
Volumetric-weighted average ∅=(∑▒〖∅i×Ai×hi 〗)/〖Ai×hi〗
Where n -
total number of core samples, hi - thickness of
core sample i or reservoir area i,
This lecture was uploaded to YouTube after formatting it in PowerPoint format PPT as a presentation. The link to the lecture #2 is on our YouTube channel - Knowledge Fields Channel here.


Comments